Psychometric Tests – Top Psychometric Testing Tips (April 2024)
Updated November 14, 2023
- A List of Psychometric Tests Available for Practice in 2024
- What Are Psychometric Tests?
- What Requirements Do All Psychometric Tests Have?
- Why are Psychometric Tests used in Recruitment?
- What Are the Different Types of Psychometric Test?
empty
empty
- What to Expect When Taking a Psychometric Test
empty
- How To Read Psychometric Test Scores?
empty
empty
empty
empty
empty
empty
- How to Interpret Psychometric Test Results?
empty
empty
- Psychometric Tests – Making Selection Decisions
empty
empty
empty
- How to Pass Psychometric Tests in April 2024
- Frequently Asked Questions
- Final Thoughts
A List of Psychometric Tests Available for Practice in 2024
- Numerical Reasoning
- Verbal Reasoning
- Diagrammatic Reasoning
- Watson Glaser
- Inductive Reasoning
- Situational Judgement
What Are Psychometric Tests?
Psychometric tests (also known as aptitude tests) attempt to objectively measure aspects of your mental ability or your personality, normally for the purposes of job selection.
The word ‘psychometric’ is formed from the Greek words for mental and measurement.
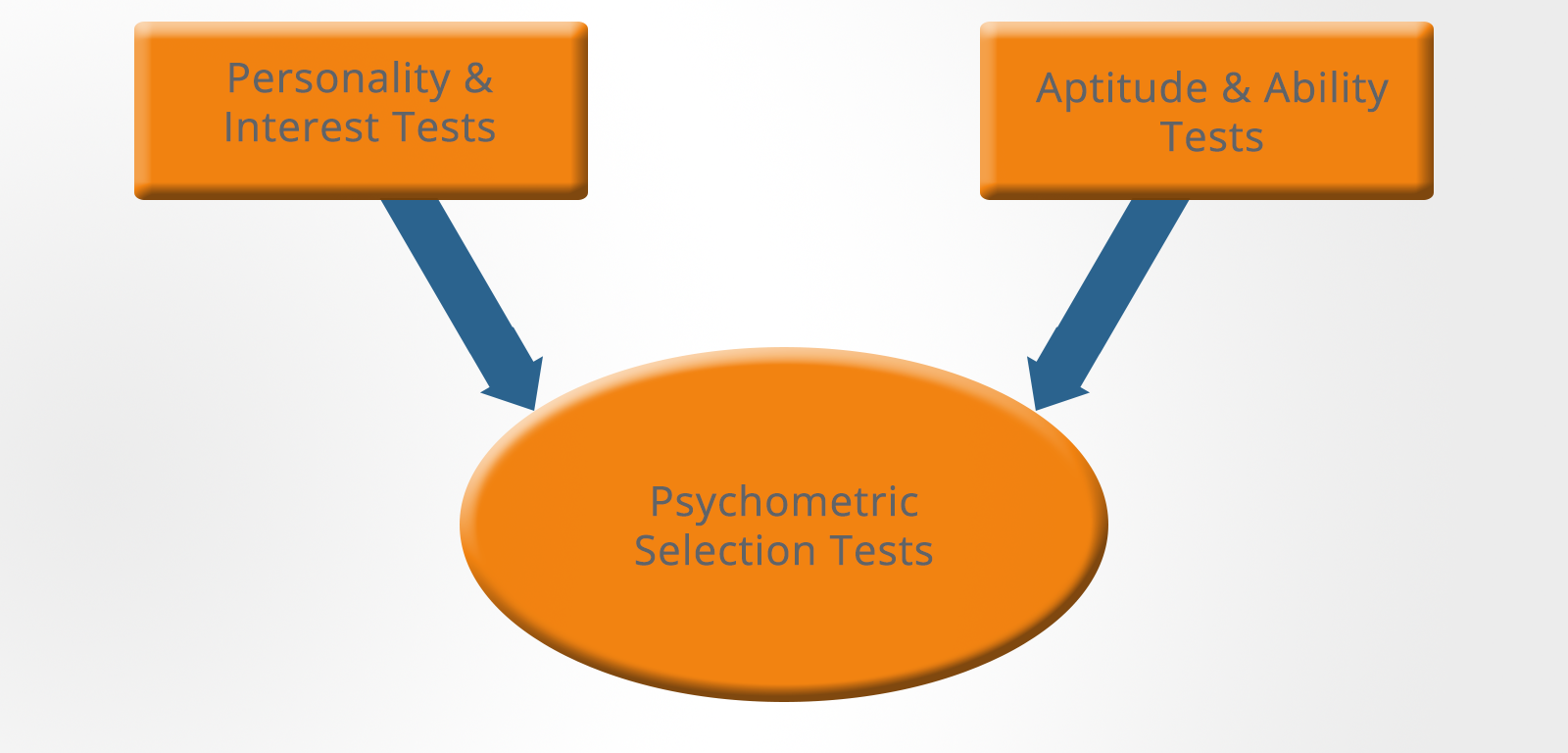
You are most likely to encounter psychometric testing as part of the recruitment or selection process and occupational psychometric tests are designed to provide employers with a reliable method of selecting the most suitable job applicants or candidates for promotion.
Psychometric tests are seldom used in isolation and represent just one of the methods used by employers in the selection process.
The usual procedures for selecting candidates still apply.
For example, a job is advertised and you are invited to send in your resume, which is then checked to see if the organization thinks that your experience and qualifications are suitable.
It is only after this initial screening that you may be asked to sit a psychometric test.
Employers typically use psychometric tests as a way of:
- Eliminating unsuitable candidates at an early stage
- Screening candidates for interviews
- Objectively determining someone’s ability, personality, motivation, values and reactions to their environments
- Identifying the strengths or weaknesses missing in existing teams and helping to make strategic recruitment decisions
- Providing management with guidance on career progression for existing employees
What Requirements Do All Psychometric Tests Have?
A psychometric test must be:
- Objective – The score must not be affected by the testers' beliefs or values.
- Standardized – It must be administered under controlled conditions. The test needs to be as consistent as possible for the test results to be accurate.
- Reliable – It must minimize and quantify any intrinsic errors.
- Predictive – It must make an accurate prediction of performance.
- Non-Discriminatory – It must not disadvantage any group on the basis of gender, culture, ethnicity, etc.
Practice Psychometric Tests with JobTestPrep
Why are Psychometric Tests used in Recruitment?
Organizations traditionally use several different methods to assess job applicants.
You will usually be asked to:
- Complete an application form
- Send in a copy of your resume
- Attend at least one interview
However, these traditional recruitment methods can be seen as flawed in several ways:
- Resumes and application forms allow a candidate to potentially exaggerate responsibilities and achievements.
- There is a growing industry in both books and online businesses which offer help in writing the perfect resume.
- The number of courses and qualifications has grown rapidly in recent years and it is not always clear what a particular qualification means in terms of abilities.
- The interview process has shortcomings since the candidate needs only to prepare for a short and relatively predictable series of questions.
- Interviewer bias can act against the interests of the recruiting organization by excluding the most capable candidate on entirely spurious grounds.
- References are notoriously unreliable as previous employers have nothing to gain by warning a potential employer of an unsuitable candidate.
Therefore, there is growing evidence that the use of psychometric tests for selection purposes has increased in recent years.
Psychometric assessment tests are now used by over 80% of the Fortune 500 companies in the US and by over 75% of the Times Top 100 companies in the UK.
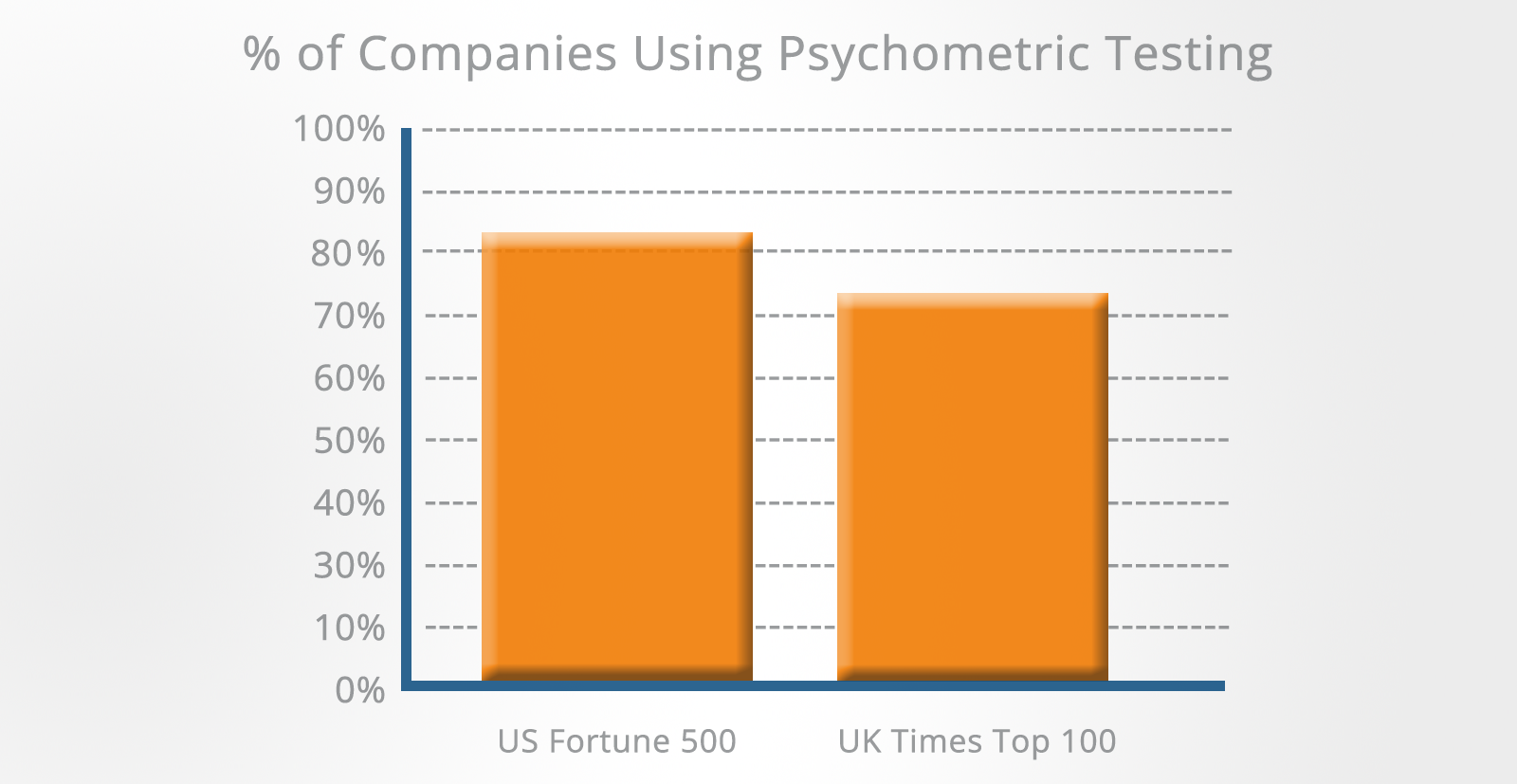
Information technology companies, financial institutions, management consultancies, local authorities, the civil service, police forces, fire services and the armed forces all make extensive use of psychometric assessment.

There are several reasons for the increase in the number of organizations using tests:
-
Increased regulation and legislation – Employers need to have a selection process that can withstand legal challenges. Psychometric tests are seen as objective measures of how a candidate’s skills align with the competency profile for the job in question.
-
Increased costs of training staff – Organizations with larger training expenditures use psychometric testing more than those with smaller training expenditures.
-
Testing costs have decreased – Increased test use is a response to the decreasing cost of testing relative to other methods of selection. This is due to more providers entering the market and to the increased use of technology, particularly the internet, in administering tests and assessing the results.
-
More formal HR policies – The increase in employment-related litigation has encouraged many organizations to recruit more highly qualified human resources personnel who tend to promote more formalized methods of selection. Psychometric testing offers some scientific credibility and objectivity to the recruitment process which otherwise can be seen as highly subjective.
-
Loss of confidence in academic qualifications – There is strong evidence for a loss of confidence in school-based formal qualifications and/or the standard of degrees. Many managers now accept that psychometric tests will provide more information on skills, such as quantitative reasoning, which complement qualification-based evidence. Aptitude tests are also seen as providing data on a variety of skills that are not suited to formal certification.
-
Screening large numbers of candidates – Psychometric tests are a quick and relatively cheap way of eliminating large numbers of unsuitable candidates very early in the recruitment process. From the perspective of human resources, psychometric testing can reduce the workload considerably as it can replace initial screening interviews which were traditionally used to shortlist candidates for a more rigorous second interview.
-
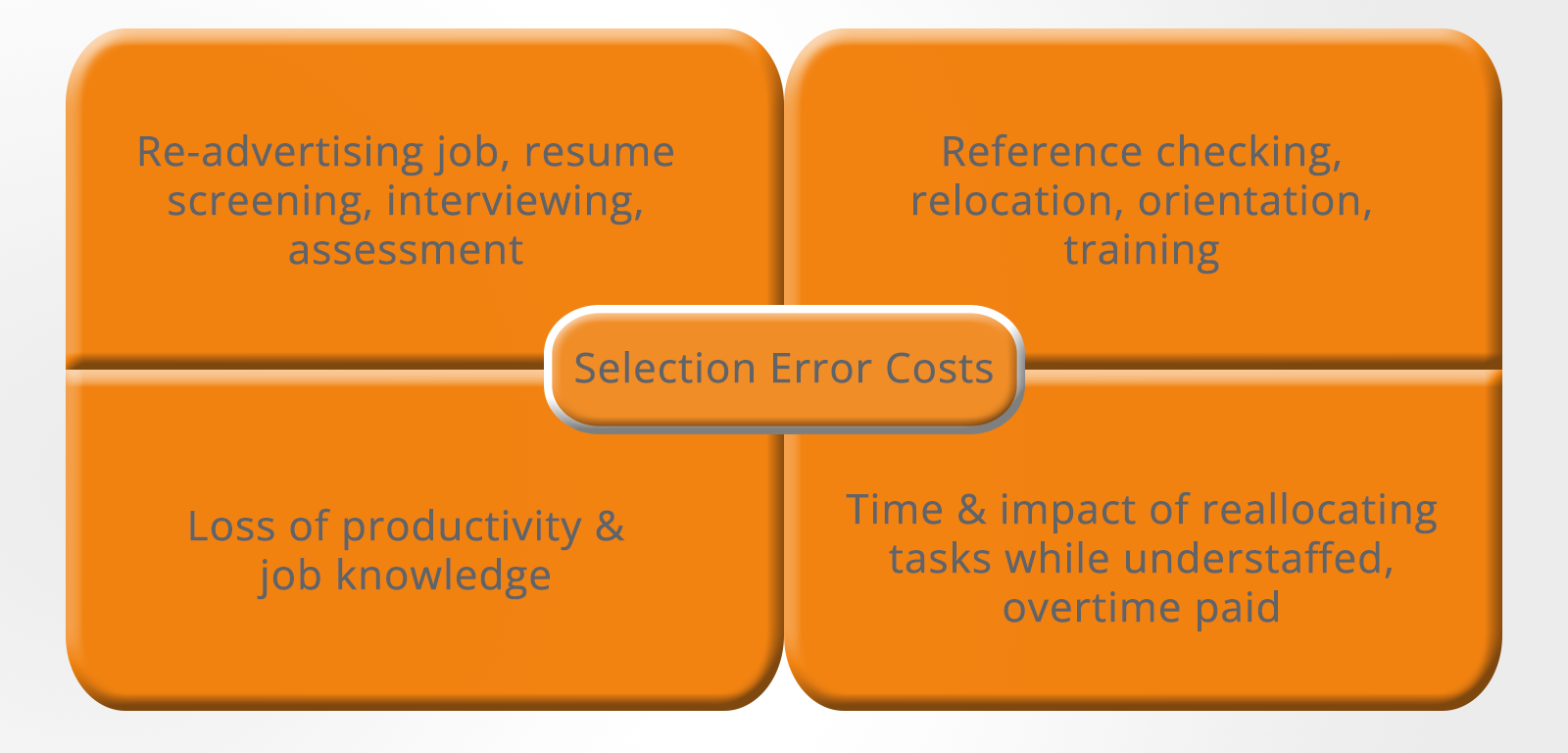
The cost of recruitment – The recruitment process is extremely expensive and time-consuming. If an organization selects the wrong candidate then the potential costs are extremely high. The overall cost of poor selection is incalculable but almost certainly equals twice the annual salary of the job incumbent – and in many jobs where severance pay is given, it will be far greater than this.
What Are the Different Types of Psychometric Test?
Psychometric tests fall into two main categories:
- Psychometric personality tests, which measure aspects of your personality
- Aptitude psychometric tests, which measure your intellectual and reasoning abilities
Psychometric Personality Tests
Personality has a significant role to play in deciding whether you have the enthusiasm and motivation that the employer is looking for and whether you are going to fit into the organization in terms of your personality, attitude and general work style.
The principle behind personality questionnaires is that it is possible to quantify your intrinsic personality characteristics by asking you about your feelings, thoughts and behavior.
You will be presented with statements describing various ways of feeling or acting and will be asked to answer each one on a two-point, five-point or seven-point scale.
The number of questions you are expected to answer varies from about 50 to 200 depending on the duration of the test.
There are supposedly no right or wrong answers and the questionnaires are usually completed without a strict time limit.
Example questions:
1. I prefer to avoid conflict
A) True
B) False
2. I enjoy parties and other social occasions
A) Strongly disagree
B) Disagree
C) Neutral
D) Agree
E) Strongly agree
3. Work is the most important thing in my life
A) Very strongly disagree
B) Strongly disagree
C) Disagree
D) Neutral
E) Agree
F) Strongly agree
G) Very strongly agree
For more on personality tests see our dedicated article.
Practice aptitude tests with JobTestPrep, where you will find interactive questions and worked solutions to help you get the job you want.
Aptitude Psychometric Tests
Aptitude and ability tests are designed to assess your intellectual performance.
There are at least 5,000 aptitude and ability tests on the market. Some of them contain only one type of question (for example, verbal ability, numerical reasoning ability, etc.) while others are made up of different types of questions.
They are always presented in a multiple-choice format and the questions have definite right and wrong answers.
They are strictly timed and to be successful you need to work through them as quickly and accurately as possible.
The different types of aptitude psychometric tests can be classified as follows:
-
Verbal ability – Includes spelling, grammar, and the ability to understand analogies and follow detailed written instructions. These questions appear in most general aptitude tests because almost all employers require job candidates with good communication skills.
-
Numerical ability – Includes basic arithmetic, number sequences and simple mathematical reasoning. In management-level tests, you will often be presented with charts and graphs that need to be interpreted. These questions appear in most general aptitude tests because employers usually want some indication of your ability to use numbers even if this is not a major part of the job.
-
Abstract/diagrammatic reasoning – Measures your ability to identify the underlying logic of a pattern and then determine the solution. Because abstract reasoning ability is believed to be the best indicator of fluid intelligence and your ability to learn new things quickly, these questions appear in most general aptitude tests.
-
Spatial ability – Measures your ability to manipulate shapes in two dimensions or to visualize three-dimensional objects presented as two-dimensional pictures. These questions are not usually found in general aptitude tests unless the job specifically requires good spatial skills.
-
Mechanical reasoning – Designed to assess your knowledge of physical and mechanical principles. Mechanical reasoning questions are used to select for a wide range of jobs including the military (Armed Services Vocational Aptitude Battery), police forces, fire services, as well as many craft, technical and engineering occupations.
-
Fault diagnosis – These tests are used to select technical personnel who need to be able to find and repair faults in electronic and mechanical systems. As modern equipment of all types becomes more dependent on electronic control systems (and arguably more complex), the ability to approach problems logically to find the cause of the fault is increasingly important.
-
Data checking – Measures how quickly and accurately errors can be detected in data and are used to select candidates for clerical and data input jobs.
-
Work sample – Involves a sample of the work that you will be expected to do. These types of tests can be very broad-ranging. They may involve exercises using a word processor or spreadsheet if the job is administrative, or they may include giving a presentation or in-tray exercises if the job is management or supervisory level.
-
Concentration tests – Used to select personnel who need to work through items of information in a systematic way while making very few mistakes.
For more on aptitude psychometric tests, see our dedicated article.
If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
What to Expect When Taking a Psychometric Test
After receiving candidates’ resumes, the organization will screen them against the job specification, discarding those where the qualifications or experience are judged to be insufficient.
The remaining candidates will each be sent a letter or email telling them when and where the psychometric testing will take place and what form it will take.
The psychometric assessment date is usually set one to two weeks after all of the resumes have been processed.
You will usually receive sample questions so that you have an idea of the type of questions used in the test.
This is to ensure that everyone has the opportunity to prepare for the test and that nobody is going to be upset or surprised when they see the test paper.
You will usually be told:
- The date, time and place of the test
- The format, duration and whether there are any breaks scheduled
- The types of psychometric test you will be given
- Any materials that will be supplied
- Whether the test is paper-based or uses a PC or palm-top computer
If you have any special requirements for the test, you must notify the test center immediately. This might include disabled access and any eyesight or hearing disability you may have.
Large text versions of the test should be available for anyone who is visually impaired and provision for written instructions should be made for anyone with a hearing disability.
Before the psychometric test begins, you can expect the test administrator to provide a thorough explanation of what you will be required to do.
You will also be given the opportunity to ask any questions before the test begins.
Whichever type of test you are given, the questions are almost always presented in multiple-choice format.
If you are taking an aptitude test, you may find that the questions become more difficult as you proceed through the test and that there are more questions than you can comfortably complete in the time allowed.

Practice Psychometric Tests with JobTestPrep
When the Test Begins
Listen carefully to the instructions and if you don’t understand something, ask.
Read the instructions for each question carefully.
If you are unsure about a question then either guess (if you don’t plan to return to it) or make a mark next to it so you can easily find it later.
Pay no attention to how any other candidate is progressing. You have nothing to gain by knowing whether they are ahead of you and you will undermine your confidence if they are.
How To Read Psychometric Test Scores?
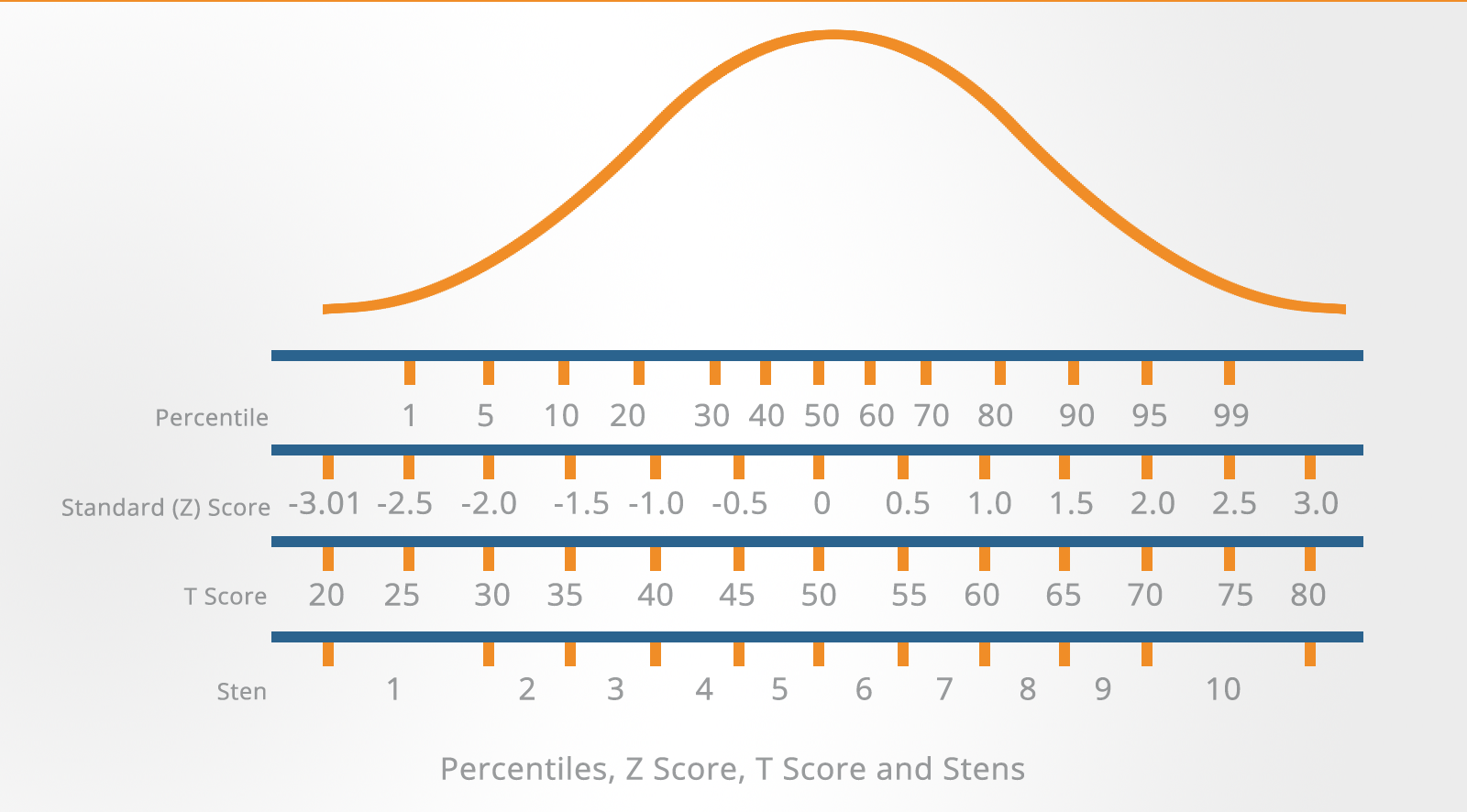
You will usually see your psychometric test results presented in terms of numerical scores.
These may be:
- Raw scores
- Standard scores
- Percentile scores
- Z-scores
- T-scores
- Stens
To interpret your scores properly, you need to understand what these mean and how they are derived:
Raw Scores
These refer to your unadjusted score. For example, the number of items answered correctly in an aptitude or ability test.
Some types of assessment tools, such as personality questionnaires, have no right or wrong answers, and in this case, the raw score may represent the number of positive responses for a particular personality trait.
Obviously, raw scores by themselves are not very useful.
If you are told that you scored 40 out of 50 in a verbal aptitude test, this is largely meaningless unless you know where your particular score lies within the context of the scores of other people.
Raw scores need to be converted into standard scores or percentiles to provide you with this kind of information.
Standard Scores
Standard scores indicate where your score lies in comparison to a norm group.
For example, if the average or mean score for the norm group is 25 then your own score can be compared to this to see if you are above or below this average.
Percentile Scores
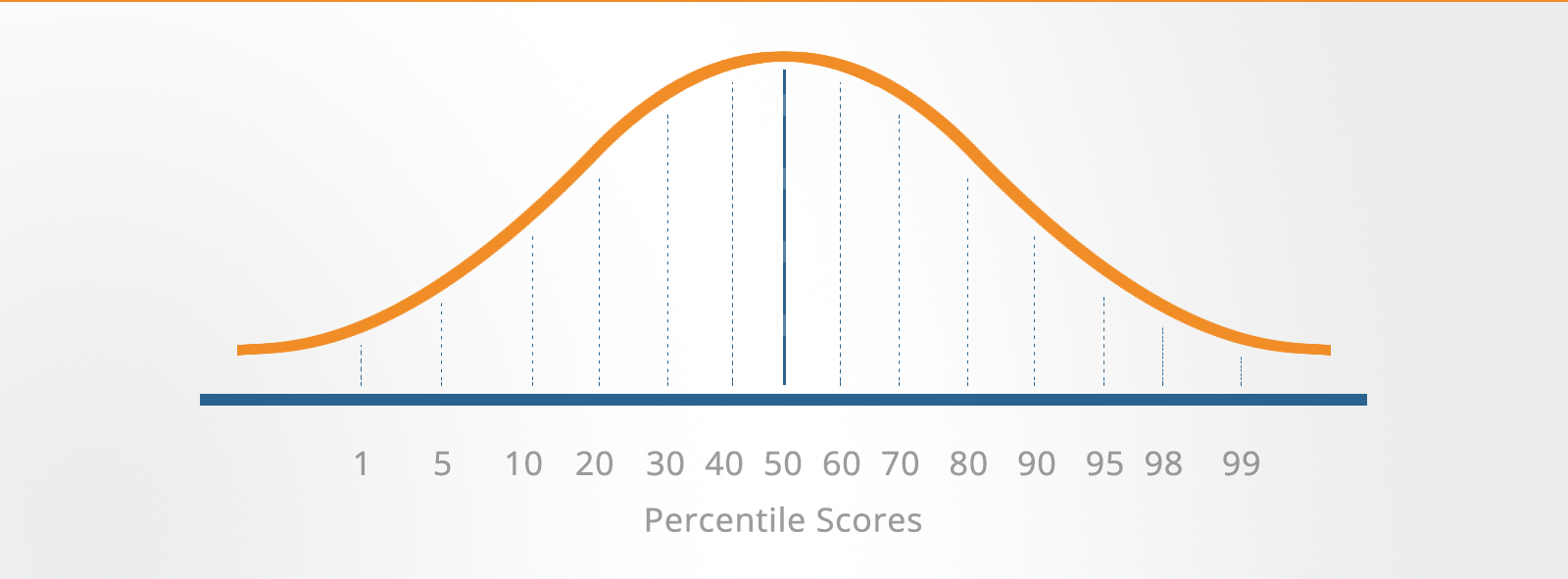
A percentile score is another type of converted score.
Your raw score is converted to a number indicating the percentage of the norm group who scored below you.
For example, a score at the 60th percentile means that the individual's score is the same as or higher than the scores of 60% of those who took the test.
The 50th percentile is known as the median and represents the middle score of the distribution.
Percentiles have the disadvantage that they are not equal units of measurement.
For instance, a difference of five percentile points between two individual’s scores will have a different meaning depending on its position on the percentile scale, as the scale tends to exaggerate differences near the mean and collapse differences at the extremes.
Percentiles can not be averaged nor treated in any other way mathematically. However, they do have the advantage of being easily understood and can be very useful when giving feedback to candidates or reporting results to managers.
Z-Scores
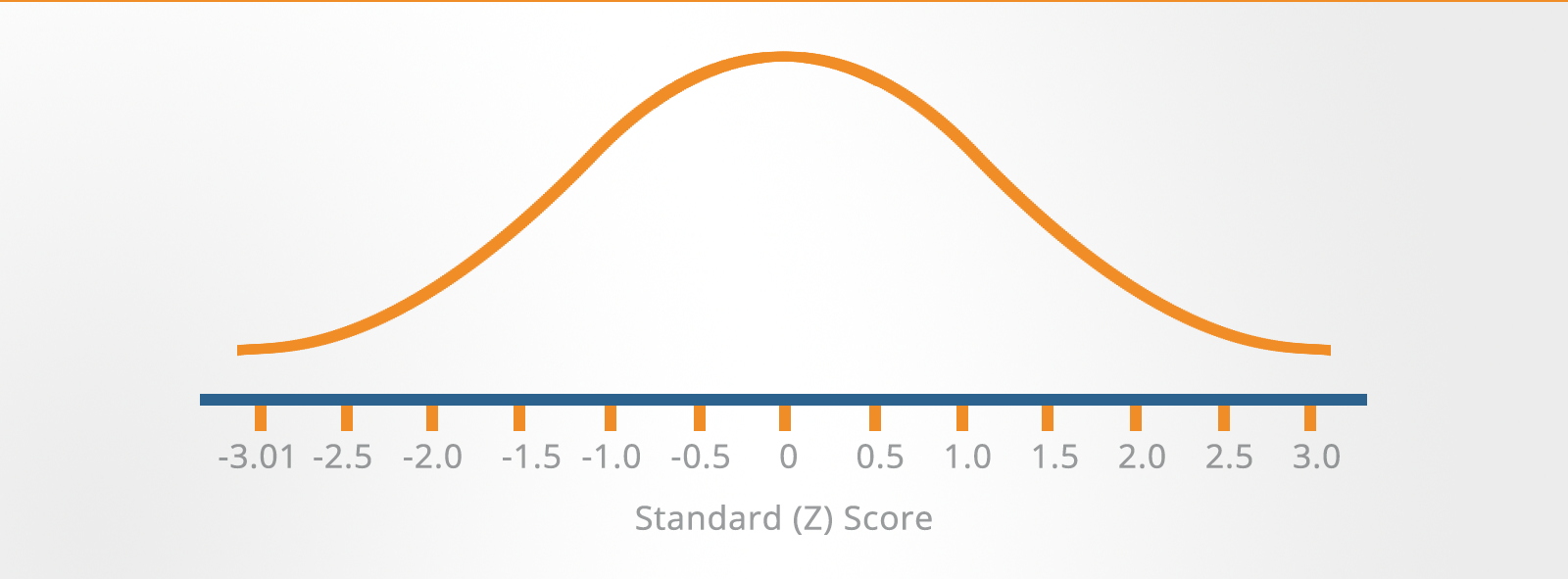
To overcome the problems of interpretation implicit with percentiles and other rank order systems, various types of standard scores have been developed.
One of these is the Z-score which is based on the mean and standard deviation. It indicates how many standard deviations above or below the mean your score is.
The Z-score is calculated by the formula: Z = X – M/SD
Where:
Z = Standard score
X = Individual raw score
M = Mean score
SD = Standard deviation
The illustration shows how Z-scores in standard deviation units are marked out on either side of the mean.
It shows where your score sits in relation to the rest of the norm group.
If it is above the mean then it is positive and if it is below the mean then it is negative.
As you can see from the illustration, Z-scores can be rather cumbersome to handle because most of them are decimals and half of them can be expected to be negative.
T-Scores (Transformed Scores)
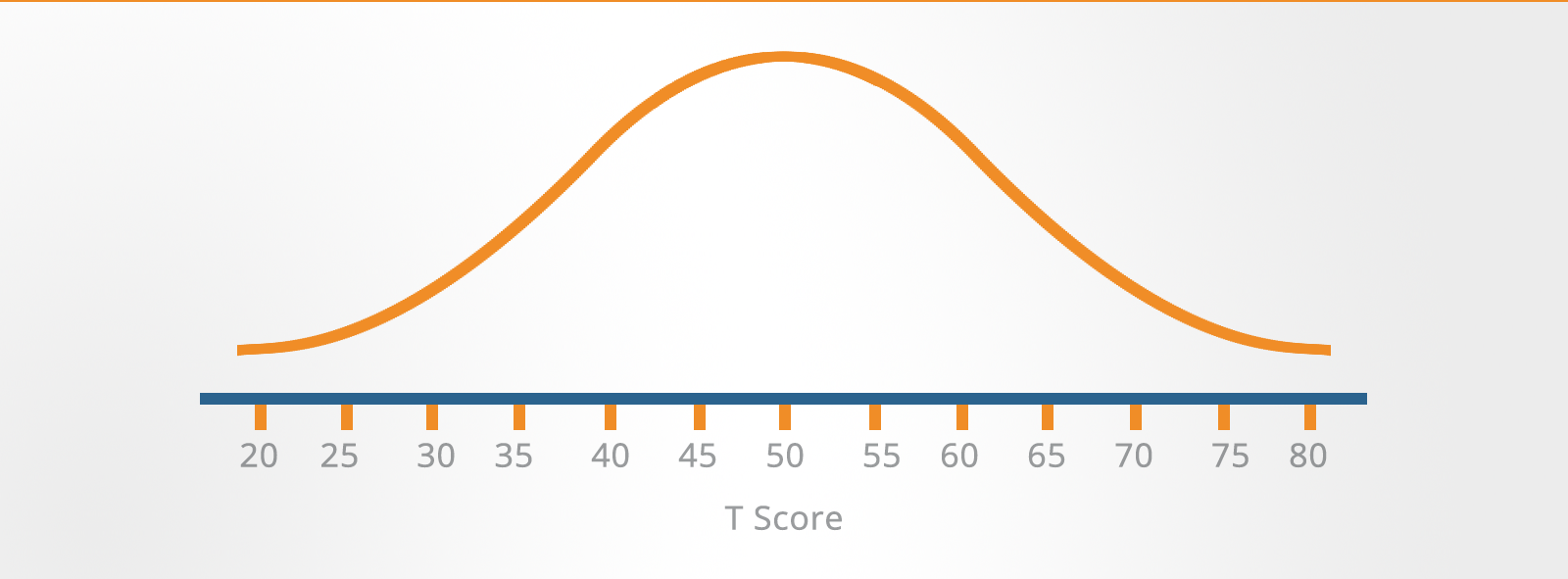
T-scores are used to solve this problem of decimals and negative numbers.
The T-score is simply a transformation of the Z-score, based on a mean of 50 and a standard deviation of 10.
A T-score can be calculated from a Z-score using the formula:
T = (Z x 10) + 50
Since T-scores do not contain decimal points or negative signs, they are used more frequently than Z-scores as a norm system, particularly for aptitude tests.
Stens (Standard Tens)

The Sten (standard ten) is a standard score system commonly used with personality questionnaires.
Stens divide the score scale into ten units.
Each unit has a bandwidth of half a standard deviation except the highest unit (Sten 10) which extends from two standard deviations above the mean, and the lowest unit (Sten 1) which extends from two standard deviations below the mean.
Sten scores can be calculated from Z-scores using the formula:
Sten = (Z x 2) + 5.5
Stens have the advantage that they enable results to be thought of in terms of bands of scores rather than absolute scores.
These bands are narrow enough to distinguish statistically significant differences between candidates but wide enough not to overemphasize minor differences between candidates.
How to Interpret Psychometric Test Results?
There are two distinct methods that employers use to interpret your Psychometric Test scores:
1. Criterion-Referenced Interpretation
In criterion-referenced tests, your Psychometric score indicates the amount of skill or knowledge that you have in a particular subject area.
The Psychometric test score is not used to indicate how well you compare to others – it relates solely to your degree of competence in the specific area assessed.
Criterion-referenced assessment is generally associated with achievement testing and certification.
A particular test score is chosen as the minimum acceptable level of competence.
This can either be set by the test publisher who will convert test scores into proficiency standards, or the company may use its own experience to do this.
For example, suppose a company needs clerical staff with word processing proficiency.
The Psychometric test publisher may provide a conversion table relating word processing skill to various levels of proficiency, or the companies own experience with current clerical employees may help them to determine the passing score.
They may decide that a minimum of 50 words per minute with no more than two errors per 100 words is sufficient for a job with occasional word processing duties.
Alternatively, if they have a job with high production demands, they may set the minimum at 100 words per minute with no more than 1 error per 100 words.
Norm-Referenced Interpretation
In norm-referenced test interpretation, your scores are compared with the test performance of a particular reference group, called the norm group.
The norm group usually consists of large representative samples of individuals from specific populations, undergraduates, senior managers or clerical workers.
It is the average performance and distribution of their scores that become the test norms of the group.
This illustration shows the distribution and mean scores for a variety of groups for a specific Psychometric test.
A score of 150 on this test would be average for someone working for the organization at an administrative level but would be below average compared to the organization’s graduate trainees, where the average score was 210.
Within the field of occupational testing, a wide variety of individuals are assessed for a broad range of different jobs.
Clearly, people vary markedly in their abilities and qualities, and the norm group against which you are compared is of crucial importance.
To make sure that the test results can be interpreted in a meaningful way, the test administrator will identify the most appropriate norm group.
This is done by comparing the educational level, occupational, language and cultural backgrounds, and other demographic characteristics of the individuals making up the two groups (norm group and test group) to establish their similarity.
Psychometric Tests – Making Selection Decisions
The rank-ordering of test results, the use of cut-off scores or some combination of the two is commonly used to assess the Psychometric test scores and make employment-related decisions about them.
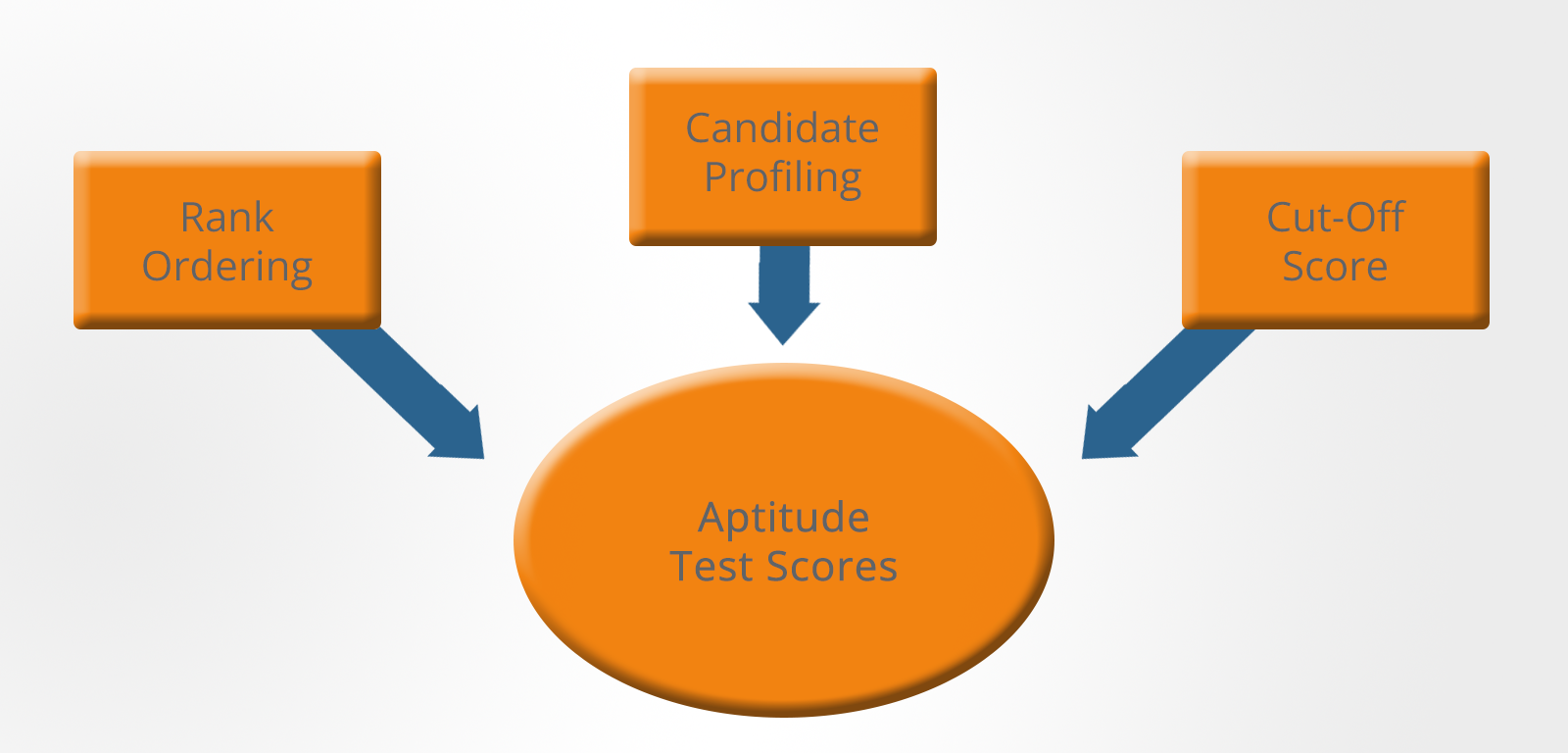
There are essentially three approaches that can be taken:
Rank Ordering
The organization could simply select the top scorers.
This would seem to be the most obvious approach but it does have a major drawback, at least where ordinary jobs are concerned.
In times of high unemployment, the job is likely to attract some candidates who are too high-powered and who will probably get bored quickly and move on as soon as they can.
Alternatively, if unemployment is very low, all of the candidates may have poor scores and may not be up to the job.
Neither of these represents a successful outcome for the organization.
Cut-Off Score
The second option is to shortlist candidates who achieve more than a minimum acceptable score.
This is more flexible than the above approach as it ensures that candidates who are not up to the job are excluded whilst giving the interviewer or decision-maker the option to exclude candidates they feel are too high powered.
Candidate Profiling
The third option is to use a minimum acceptable score in conjunction with profiling.
This approach first excludes unsuitable candidates on the basis of minimum score and then takes into account the relative strengths of each suitable candidate in all of the areas in which they have been tested.
This is then used to produce a profile map that can be compared to the ideal profile for the job.
This profile will be based on a job specification compiled by an occupational psychologist, or qualified personnel professional.
This job specification will encompass the following areas:
- Knowledge – Is specific knowledge needed? For example, medical, legal, financial, engineering, etc. This will often be decided on the basis of recognized qualifications but will be influenced by previous job experience.
- Skills – Are specific skills needed? For example, typing 150 words per minute, ability to operate a CNC machine, etc. This will often be decided on the basis of recognized qualifications but will be influenced by previous job experience.
- Abilities – Are underlying abilities needed? For example, numerical ability, artistic ability, problem-solving ability. These may be decided on the basis of aptitude or ability tests.
- Experience – Is specific experience necessary? For example, managing a construction project.
- Personal qualities – Are particular qualities required? For example, interpersonal skills or leadership skills.
How to Pass Psychometric Tests in April 2024
You may hear people say that it is not possible to prepare for psychometric tests.
This is simply untrue.
You can significantly improve your scores in aptitude tests especially by practicing the types of questions that you will face.
Even with personality questionnaires, spending time looking at sample questions and thinking about how you would answer them in relation to the expectations of the job you are applying for can be highly beneficial.
You should make your own decision about which types of questions to practice. You could either concentrate on your weakest area or you could try to elevate your score across all areas.
Whichever strategy you choose – keep practicing.
Because of the way that aptitude tests are marked, even small improvements to your raw score will have a big influence on your chances of getting the job.
Research suggests that the amount of improvement you can expect will depend on three areas:
-
Your educational background – The longer that you have been out of the educational system and the less formal your educational background, the more likely you are to benefit from practice. Both of these factors suggest that familiarity with any type of examination process, both formal and timed, will give you an advantage.
-
Your personal interests – Most people who have been out of education for more than a few years will have forgotten how to multiply fractions and calculate volumes. While it is easy to dismiss these as 'first grade' or elementary maths, most people simply don't do these things on a day-to-day basis unless their job or a hobby demands it. Practice will refresh these dormant skills.
-
The quality of the practice material – The material itself needs to match as closely as possible the tests that you expect to take. If you are unfamiliar with the types of test questions, you will waste valuable time trying to determine what exactly the questions are asking you to do. This unfamiliarity also causes you to worry about whether you have understood the question correctly and this also wastes mental energy. By increasing your familiarity with the style and types of questions, you will improve your scores.
Here are our top psychometric testing tips for success:
Step 1. Control Your Nerves
It is perfectly normal to feel some stress and nervousness when you are told that you need to take a psychometric test.
Most of the nervousness is simply a fear of the unknown.
You will hear a lot of advice for coping with the symptoms of stress and anxiety, including relaxation, exercise and visualization.
While all of these things can help, the most effective solution is to take direct action and spend your time practicing psychometric tests in the most systematic and efficient way possible.
Step 2. Don’t Make Assumptions About Your Own Abilities
Many people assume that they won't have any problems with verbal ability questions, for example, because they once got an 'A' in an English exam.
They may have a point if they got the 'A' a few months ago, but what if it was 10 years ago?
The same thing applies to numerical ability. Don't assume anything – it's better to do some practice tests and then you'll know for sure.
Step 3. Practice in Real Exam Conditions
Find somewhere where you will not be disturbed, go through each paper without interruption and try to stick to the time limit.
Do not have anything with you that’s not allowed on the day of the test and switch off your mobile phone.
If you don’t have an uninterrupted twenty minutes for a practice paper, try to complete the first half of the questions in 10 minutes and treat the second half as another 10-minute paper.
Concentrate one hundred percent for the duration of the test as this keeps the practice as realistic as possible.
Practice Psychometric Tests with JobTestPrep
Employers looking to assess whether a candidate demonstrates a specific ability may use a Psychometric test as part of their recruitment process.
Psychometric tests, also known as aptitude tests, provide an objective measure of a candidate's ability or personality in a specific area as relevant to the requirements of a role.
Using psychometric tests in a recruitment process helps employers select the best candidates for the positions they have to fill.
To enable employers to measure a specific ability or aptitude objectively, psychometric assessments need to be objective, standardized, reliable, non-discriminatory and predictive.
Ensuring these criteria are met when creating and devising a test ensures that the test can be used alongside other elements of a recruitment process to provide a holistic view of a candidate's ability or aptitude in a particular area.
When devising a recruitment and selection process, employers will determine the abilities required for their recruiting role. The employer will then select any relevant ability or personality tests to ensure a fair and transparent recruitment process.
Employers will generally provide you with practice tests if you are invited to sit a psychometric test as part of the recruitment process.
Ensuring you have attempted these practice tests is advisable before taking the test itself.
You can also find additional practice psychometric tests on the JobTestPrep website.
Preparation is vital to ensuring you perform at your best when sitting a psychometric test.
Practice as many psychometric tests as you can to ensure you are familiar with the layout and the style of questioning. Practice all types of ability tests so you can identify any gaps in your understanding that you may need to refresh your memory on.
Ensuring your practice tests under timed conditions will help simulate the time pressure you will feel in the actual test and help you understand how to control your nerves.
A psychometric test is an ability test that enables employers to determine whether you possess the abilities required for success in a role.
Assessments are generally timed, comprise a set number of questions, and can be taken online or as a paper and pencil test, depending on an employer's recruitment process format.
When used alongside other stages of the recruitment process, a psychometric assessment allows employers to gain an objective view of the level of aptitude you have in a particular area to predict whether you will be successful in a role.
Many psychometric test providers provide bespoke tests to employers. These tests vary in format and structure, with employers selecting the provider that best suits their requirements when considering their overall recruitment process.
If you are invited to take a psychometric test by an employer, it is advisable to practice.
You can find several practice tests on the Psychometric Success website, along with hints and tips on how to perform at your best when taking a psychometric test.
The best way to prepare for a psychometric test is to practice. When practicing, ensure you simulate test conditions. This means practicing under timed conditions, in a quiet room, and free from distractions.
Ensure you practice as many tests as you can so you become familiar with the format and the style of questioning and how you react under time pressure.
A good way to practice is via the Psychometric Success app, available on Apple and Android devices.
Employers use various types of online psychometric tests as part of their recruitment process.
If you are invited to sit a psychometric assessment, ensure you take practice tests as part of your preparation.
You can find many psychometric tests on the JobTestPrep website.
These practice tests have been designed to provide a realistic experience of the question types you may face when sitting employers' online psychometric tests.
Each employer will have their own way of scoring a psychometric assessment. Scores are generally presented as numerical scores in different formats. These can be as a percentile, a Z score, raw score. T score or sten score.
Scores are then interpreted according to a candidate's skill level or by comparing your score to other candidates who have previously taken the test (known as a norm group).
When sitting a psychometric assessment, focus on performing at your best and answering as many questions as you can answer correctly in the given time limit.
The basis of a psychometric assessment is to provide an objective and reliable assessment of a candidate's ability in a specific area.
Scores from psychometric tests are used differently depending on the employer's recruitment process. Some employers will use candidates' scores to determine their skill level. Others will take a candidate's scores and compare these to a population of candidates who have previously taken the test.
Whatever the scoring method, the results from a psychometric assessment are used alongside the various stages of an employer's recruitment process. These overall results provide a reliable indication of a candidate's suitability for the role they have applied for.
Preparation is vital to ensure you perform at your best in a psychometric test. Preparing for a psychometric test means practicing as many tests as you can.
You can find lots of advice, hints, tips and practice tests on the Psychometric Success website and app available on Android and Apple devices.
If you are invited to sit a psychometric test as part of an employer's recruitment process, you will often be sent practice tests in your invitation.
To ensure you perform at your best, it is advisable to practice as many tests as you can. You can find lots of advice and guidance on sitting psychometric tests on the Psychometric Success app available on both Apple and Android devices.
There are many kinds of psychometric tests; each test focuses on the assessment of a different ability.
In addition, employers may use personality tests as part of their recruitment process to better understand a candidate's characteristics, traits or behaviors when in the workplace.
If you are invited to take a psychometric test, ensure you are clear on the type of test and what ability the test is assessing.
Final Thoughts
Want to try some practice Psychometric Tests?
An excellent way to practice is via the Psychometric Tests app: available for both Android and Apple devices.






